二次函数的定义：

一般地，如果（a，b，c是常数，a≠0），那么y叫做x的二次函数。

二次函数的图像：

是一条关于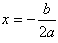对称的曲线，这条曲线叫抛物线。
抛物线的主要特征：①有开口方向，a表示开口方向；a＞0时，抛物线开口向上；a<0时，抛物线开口向下；
②有对称轴；
③有顶点；
④c表示抛物线与y轴的交点坐标：（0，c）。

性质：二次函数y=ax²+bx+c，

①当a＞0时，函数f（x）的图象开口向上，在（-∞，-）上是减函数，在[-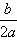，＋∞）上是增函数；
②当a<0时，函数f（x）的图象开口向下，在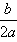（-∞，-）上是增函数，在[-，＋∞）是减函数。

二次函数（a，b，c是常数，a≠0）的图像：

图像	函数的性质
a>0	定义域	x∈R(个别题目有限制的，由解析式确定)
	值域	a>0	a<0
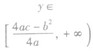	奇偶性	b=0时为偶函数，b≠0时为非奇非偶函数
a<0	单调性	a>0	a<0
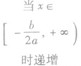	图像特点

二次函数的解析式：

（1）一般式：（a，b，c是常数，a≠0）；
（2）顶点式：若二次函数的顶点坐标为（h,k），则其解析式为;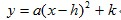
（3）双根式：若相应一元二次方程的两个根为 ,则其解析式为 。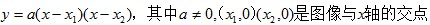

二次函数在闭区间上的最值的求法：

(1)二次函数在区间[p,g]上的最值问题
一般情况下，需要分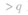三种情况讨论解决．
当a>0时，f(x)在区间[p，g]上的最大值为M，最小值为m，令．
①
②
③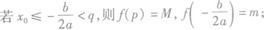
④
特别提醒：在区间内同时讨论最大值和最小值需要分四种情况讨论．

(2)二次函数在区间[m．n]上的最值问题一般地，有以下结论：

特别提醒：max{1,2}=2,即取集合{1,2}中最大的元素。

二次函数的应用：

（1）应用二次函数才解决实际问题的一般思路：
理解题意；建立数学模型；解决题目提出的问题。
（2）应用二次函数求实际问题中的最值：
即解二次函数最值应用题，设法把关于最值的实际问题转化为二次函数的最值问题，然后按求二次函数最值的方法求解。求最值时，要注意求得答案要符合实际问题。

本文来自：逍遥右脑记忆 http://www.jiyifa.net/gaoer/495515.html

相关阅读：高三地理二模试题2014