比较法分类:
(1)求差比较法:要证a>b,只要证a-b>0;
(2)求商比较法:要证a>b,且b>0,只要证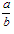 >1;
>1;
比较法的步骤是:
作差(商)后通过分解因式、配方、通分等手段变形判断符号或与1的大小,然后作出结论。
实数比较大小的依据:
在数轴上不同的点A与点B分别表示两个不同的实数a与b,右边的点表示的数比左边的点表示的数大,从实数减法在数轴上的表示可以看出a、b之间具有以下性质:如图,如果a-b是正数,那么a>b;如果a-b是负数,那么a<b;如果a-b等于零,那么a=b,反之也成立,从而a-b>0等价于a>b;a-b=0等价于a=b;a-b<0等价于a<b.
比较数(式)的大小常用的方法:
(1)一是利用作差法来判断差的符号;二是利用作商法(分母为正时)来判断商与1的大小。这两种方法的关键是变形,常用的变形的技巧有因式分解、通分、配方、有理化等,当两个代数式正负不确定且为多项式形式时常用作差法比较大小.当两个代数式均为正且为幂的乘积式时常用作商法比较大小.
(2)比较大小时应熟记并应用“若a>b且ab>0则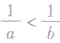 ”这一结论,不能强化也不能弱化条件,在此时应引起特别重视。
”这一结论,不能强化也不能弱化条件,在此时应引起特别重视。
相关高中数学知识点:综合法与分析法证明不等式
综合法:
利用某些已知的不等式或已证过的不等式或不等式的性质推导出所要证的不等式成立,这种证明方法叫综合法,即由因导果。利用均值不等式的有关公式最为常见。
分析法:
(1)从求证的不等式出发,分析使这个不等式成立的充分条件,把证明这个不等式的问题转化为这些条件是否具备的问题,如果能肯定这些条件都已具备,那么就可以判定所证的不等式成立,这种证明方法叫分析法,即执果索因;
(2)用分析法证明要注意格式:“若A成立,则B成立”的模式是:欲证B为真,只需证C为真,只需证D为真…最后得出A或已知的性质、公理、定理,从而得出B为真。也可使用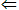 简化叙述。即B
简化叙述。即B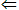 C
C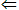 D
D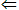 …
…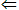 A或已知的性质、公理、定理。切不可使用B
A或已知的性质、公理、定理。切不可使用B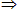 C
C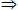 D
D …
…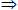 A。
A。
用综合法分析法证明不等式常用到的结论:


 3,
3,
相关高中数学知识点:反证法与放缩法
反证法的定义:
有些不等式无法利用题设的已知条件直接证明,我们可以用间接的方法——反证法去证明,即通过否定原结论——导出矛盾——从而达到肯定原结论的目的。
放缩法的定义:
把原不等式放大或缩小成一个恰好可以化简的形式,比较常用的方法是把分母或分子适当放大或缩小(减去或加上一个正数)使不等式简化易证。
反证法证题的步骤:
若A成立,求证B成立。
共分三步:
(1)提出与结论相反的假设;如负数的反面是非负数,正数的反面是非正数即0和负数;
(2)从假设出发,经过推理,得出矛盾;(必须由假设出发进行推理否则不是反证法或证错);
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.矛盾:与定义、公理、定理、公式、性质等一切已有的结论矛盾甚至自相矛盾。
反证法是一种间接证明命题的基本方法。在证明一个数学命题时,如果运用直接证明法比较困难或难以证明时,可运用反证法进行证明。
放缩法的意义:
放缩法理论依据是不等式的传递性:若,a<b,b<c,则a<c.
放缩法的操作:
若求证P<Q,先证P<P1<P2<…<Pn,再证恰有Pn<Q.
需注意:(1)只有同方向才可以放缩,反方向不可。
(2)不能放(缩)得太大(小),否则不会有最后的Pn<Q.
本文来自:逍遥右脑记忆 http://www.jiyifa.net/gaozhong/272368.html
相关阅读:数学课堂导语的作用



