定理：
如果a，b，c∈R，那么
，当且仅当a=b=c时，等号成立；
推广：
对于n个正数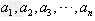
，它们的算术平均不小于它们的几何平均，即
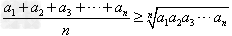，（当且仅当
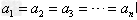时，等号成立）。
三个正数的算术、几何平均数不等式求最值：
设x,y,z都是正数，则有：
(1)若xyz=S（定值），则当x=y=z时，x+y+z有最小值，最小值为
。
(2)若x+y+z=P（定值），则当x=y=z时，xyz有最大值，最大值为
。
注：一正、二定、三等。
本文来自：逍遥右脑记忆 http://www.jiyifa.net/gaozhong/466062.html
相关阅读：高中数学七大数学基本思想方法