空间向量的正交分解的定义：

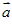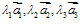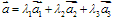对空间的任意向量，均可分解为不共面的三个向量，使，如果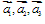两两垂直，这种分解就是空间向量的正交分解。

空间向量的坐标表示：

在空间直角坐标系O—xyz中，对空间任一点A，存在唯一的有序实数组（x，y，z），使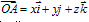，有序实数组（x，y，z）叫作向量A在空间直角坐标系O—xyz中的坐标，记作A（x，y，z），x叫横坐标，y叫纵坐标，z叫竖坐标。

空间向量基本定理：

如果三个向量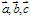不共面，那么对空间任一向量，存在一个唯一的有序实数组x，y，z，使。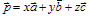
若三向量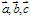不共面，我们把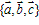叫做空间的一个基底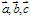，叫做基向量，空间任意三个不共面的向量都可以构成空间的一个基底。

推论：

设O，A，B，C是不共面的四点，则对空间任一点P，都存在唯一的三个有序实数x，y，z，使。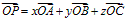

基底在向量中的应用：

(l)用基底表示出相关向量来解决向量问题是常用的方法之一．
(2)在空间中选择基底主要有以下几个特点：①不共面；②有公共起点；③其长度及两两夹角已知．(3)用基底表示向量，就是利用向量的加法和减法对有关向量进行分解。

用已知向量表示未知向量：

用已知向量表示未知向量，一定要结合图像，可从以下角度如手：
（1）要用基向量意识，把有关向量尽量统一到基向量上来；
（2）把要表示的向量标在封闭的图形中，表示为其它向量的和或差的形式，进而寻找这些向量与基向量的关系；
（3）用基向量表示一个向量时，如果此向量的起点是从基底的公共点出发的，一般考虑用加法，否则用减法，如果此向量与一个易求向量共线，可用数乘。

本文来自：逍遥右脑记忆 http://www.jiyifa.net/gaozhong/586009.html

相关阅读：2014年高考数学的答题技巧