双曲线的离心率的定义：

(1)定义：双曲线的焦距与实轴长的比叫做双曲线的离心率．
(2)e的范围：e>l．
(3)e的含义：e是表示双曲线开口大小的一个量，e越大开口越大．

渐近线与实轴的夹角也增大。

双曲线的性质：

1、焦点在x轴上：顶点：（a，0），（-a，0）；焦点：（c，0），（-c，0）；
渐近线方程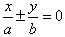：或。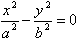
2、焦点在y轴上：顶点：（0，-a），（0，a）；焦点：（0，c），（0，-c）；
渐近线方程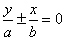：或。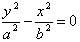
3、轴：x、y为对称轴，实轴长为2a，虚轴长为2b，焦距2c。
4、离心率；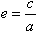
5、中，取值范围：x≤-a或x≥a，y∈R，对称轴是坐标轴，对称中心是原点。

双曲线的焦半径：

双曲线上的点之间的线段长度称作焦半径，分别记作

关于双曲线的几个重要结论：

(1)弦长公式（与椭圆弦长公式相同）．
(2)焦点三角形：已知的两个焦点，P为双曲线上一点（异于顶点），
的面积为
在解决与焦点三角形有关的问题时，应注意双曲线的两个定义、焦半径公式以及三角形的边角关系、正弦定理等知识的综合运用，还应注意灵活地运用平面几何、三角函数等知识来分析解决问题．
(3)基础三角形：如图所示，△AOB中，

(4)双曲线的一个焦点到一条渐近线的距离等于虚半轴长．
(5)自双曲线的焦点作渐近线的垂线，垂足必在相应的准线上，即过焦点所作的渐近线的垂线，渐近线及相应准线三线共点．
(6)以双曲线的焦半径为直径的圆与以实轴为直径的圆外切或内切．
(7)双曲线上一点P(x₀，y₀)处的切线方程是
(8)双曲线划分平面区域:对于双曲线,我们有：P(x₀，y₀)在双曲线内部（与焦点共区域) P(x₀，y₀)在双曲线外部（与焦点不其区域)

本文来自：逍遥右脑记忆 http://www.jiyifa.net/gaozhong/658071.html

相关阅读：高中数学学习方法要科学