函数的连续性定义：

（1）如果函数y=f（x）在点x=x₀处及其附近有定义，并且满足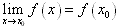，则称函数y=f（x）在点x=x₀处连续；否则称y=f（x）在点x=x₀处不连续，或间断点。
（2）如果函数f（x）在某一开区间（a，b）内每一点处都连续，就说函数f（x）在开区间（a，b）内连续，对于闭区间[a，b]上的函数f（x），如果在开区间（a，b）内连续，在左端点x=a处有，在右端点x=b处有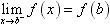，就说函数f（x）在闭区间[a，b]上连续。
3、如果f（x）是闭区间[a，b]上的连续函数，那么在闭区间[a，b]上f（x）一定有最大值和最小值。

函数的连续性的特点：

（1）f（x）在x₀处有定义；
（2）f（x）在x₀处的极限存在；
（3）f（x）在点x₀处的极限等于函数值。
三大特点，缺一不可。

常用结论：

如果f（x）是闭区间[a，b]上的连续函数，那么在闭区间[a，b]上f（x）一定有最大值和最小值。

本文来自：逍遥右脑记忆 http://www.jiyifa.net/gaozhong/718266.html

相关阅读：高中数学应该如何学

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容，请发送邮件至 4509422@qq.com 举报，一经查实，本站将立刻删除。