极差：

一组数据中最大值与最小值的差；

组距：

力求“取整”。

组数、组距、极差之间的关系：

极差＝最大值－最小值，极差又称为全距。组数＝组距/极差

作频率分布直方图的步骤：

①求极差，即一组数据中最大值和最小值的差。
②决定组距与组数．将数据分组时，组数应力求合适，以使数据的分布规律能较清楚的呈现出来。这时应注意：a．一般样本容量越大，所分组数越多；b．为方便起见，组距的选择应力求“取整”；c．当样本容量不超过100时，按照数据的多少，通常分成5组～l2组．
③将数据分组．
④计算各小组的频率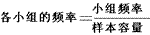（），作频率分布表。
⑤画频率分布直方图。

相关高中数学知识点：标准差、方差

方差和标准差的定义：

考察样本数据的分散程度的大小，最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离，一般用s表示。
设一组数据的平均数为，则，其中s²表示方差，s表示标准差。

一般地，平均数、方差、标准差具有如下性质：

若数据的平均数是，方差为s²，标准差为s.则新数据的平均数是a＋b，方差为，标准差为
特别地，如a＝1，则新数据的方差、标准差与原数据相同，分别为s²，s。因此，当一组数据均较大且接近某个常数时，可先将每个数同时减去这个常数，再计算这组新数据的方差，它与原数据的方差相等.

方差和标准差的意义：

方差和标准差都是用来描述一组数据波动情况的特征数，常数来比较两组数据的波动大小，方差较大的波动较大，方差较小的波动较小。

用样本的数字特征估计总体的数字特征分两类：

①用样本平均数估计总体平均数．
②用样本方差、标准差估计总体方差、标准差．样本容量越大，估计就越精确．

计算标准差的算法：

(1)算出样本数据的平均数；
(2)算出每个样本数据与样本平均数的差;
(3)算出
(4)算出这n个数的平均数，即为样本方差s²；
(5)算出方差的算术平方根，即为样本标准差s.

本文来自：逍遥右脑记忆 http://www.jiyifa.net/gaozhong/837000.html

相关阅读：高考数学导数应用题型解题方法