正态分布的定义：

如果随机变量ξ的总体密度曲线是由或近似地由下面的函数给定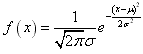：，x∈R，则称ξ服从正态分布，这时的总体分布叫正态分布，其中μ表示总体平均数，σ叫标准差，正态分布常用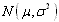来表示。
当μ＝0，σ＝1时，称ξ服从标准正态分布，这时的总体叫标准正态总体。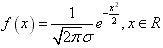
叫标准正态曲线。

正态曲线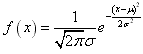，x∈R的有关性质：

（1）曲线在x轴上方，与x轴永不相交；
（2）曲线关于直线x＝μ对称，且在x＝μ两旁延伸时无限接近x轴；
（3）曲线在x＝μ处达到最高点；
（4）当μ一定时，曲线形状由σ的大小来决定，σ越大，曲线越“矮胖”，表示总体分布比较离散，σ越小，曲线越“瘦高”，表示总体分布比较集中。

在标准正态总体N（0，1）中：

（1）；
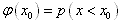（2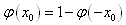）（因为曲线关于y轴对称）；
（3），。

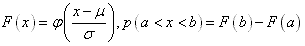本文来自：逍遥右脑记忆 http://www.jiyifa.net/gaozhong/969718.html

相关阅读：浅谈数学教学中如何运用多媒体技术